詳細は、Houtao Deng、Ganesh Krishnan、Ji Chen、Dong Liangが作成した技術レポートにあります

需要予測は、企業が将来の需要を予測し、供給を計画するのに役立ちます。実際の需要と計画された供給不一致の場合、不均衡を減らすために、価格設定などの需要形成戦略を使用することができます。

需要予測

この記事では、予測プロセスにおける伸縮需要（需要形成に対応した需要）を検討することを提案します。過去のデータに弾力的な需要を再配分して分散を最小限に抑え、より効果的な予測につなげる方法を提示します。

例えば、Instacartは昔のデータをベースにして、時間帯別の需要を予測します。下記の図１（左）をご覧ください。

そして下記は先の時間に対する需要を予測したものです（例：10–11 am）。

・時間を全体のデータから抜き取る。図1 (右) は10–11この時間帯である需要です（１０日間）。

・タイムシリーズモデル（time series model）を使って、時間帯別の重要を予想する。

左：過去10日間の1時間ごとの需要（説明のためにデータをシミュレート）。

右：過去10日間の10-11時の需要。

需要変動

しかし、このタイムシリーズモデルはトレンドや需要の季節要因を捉えたとしても、依然として説明できない大きな変動が存在する可能性があります。図1 (右) を見ればわかると思います。10–11 amこの時間帯の需求について、明確なトレンドや季節による影響は少ないですが、説明できない変動（variance）がたくさんあります。図２は図1のデータが時間帯による各時間の需要変化（demand variability）を下記にてご覧にいただけます。

図2. 1時間あたりの需要の変動（ボックスは第1四分位から第3四分位まで）。

予測と供給計画に及ぼす変動の影響は下記に示します。Table 1 は既存の二つの需要パターンです（各自は50%の可能性があります）。パターン１が示すのは9–10この間は10件の需要があります。10–11amは30件、そして、パターン２は二つの時間帯とも２０件の需要があることです。

でも両方の予測を見てください。一つは二つパターンの平均を使います。もう一つはパターン１だけ使います。

                           表1. 50％の確率 それぞれの歴史的需要パターン。

1つの供給単位が1単位の需要に役立ち、1単位の需要を失う、または1単位の過剰供給を維持するコストは1であると仮定する.2つの予測の予想コストを表2にてご覧にいただけます。

二つのコスト合計は１０です。この変動によって、ゼロコスト予測は一見不可能になります。

                                            表2.  2つの予測の予想コスト。

弾力的な需要　

状況によっては、特定の顧客が製品/サービスオプションに柔軟に対応できるため、価格設定などの需要形成戦略が選択肢に影響する可能性があります。要求を形成する戦術に応答する要求は、伸縮需要と呼ばれます。

ここで一つ注意しなければならない点は、昔の注文は需要形成の影響を受けています。ある商品の数と値段で需要の形成を行わずに顧客が選択した選択肢を推測することができます。

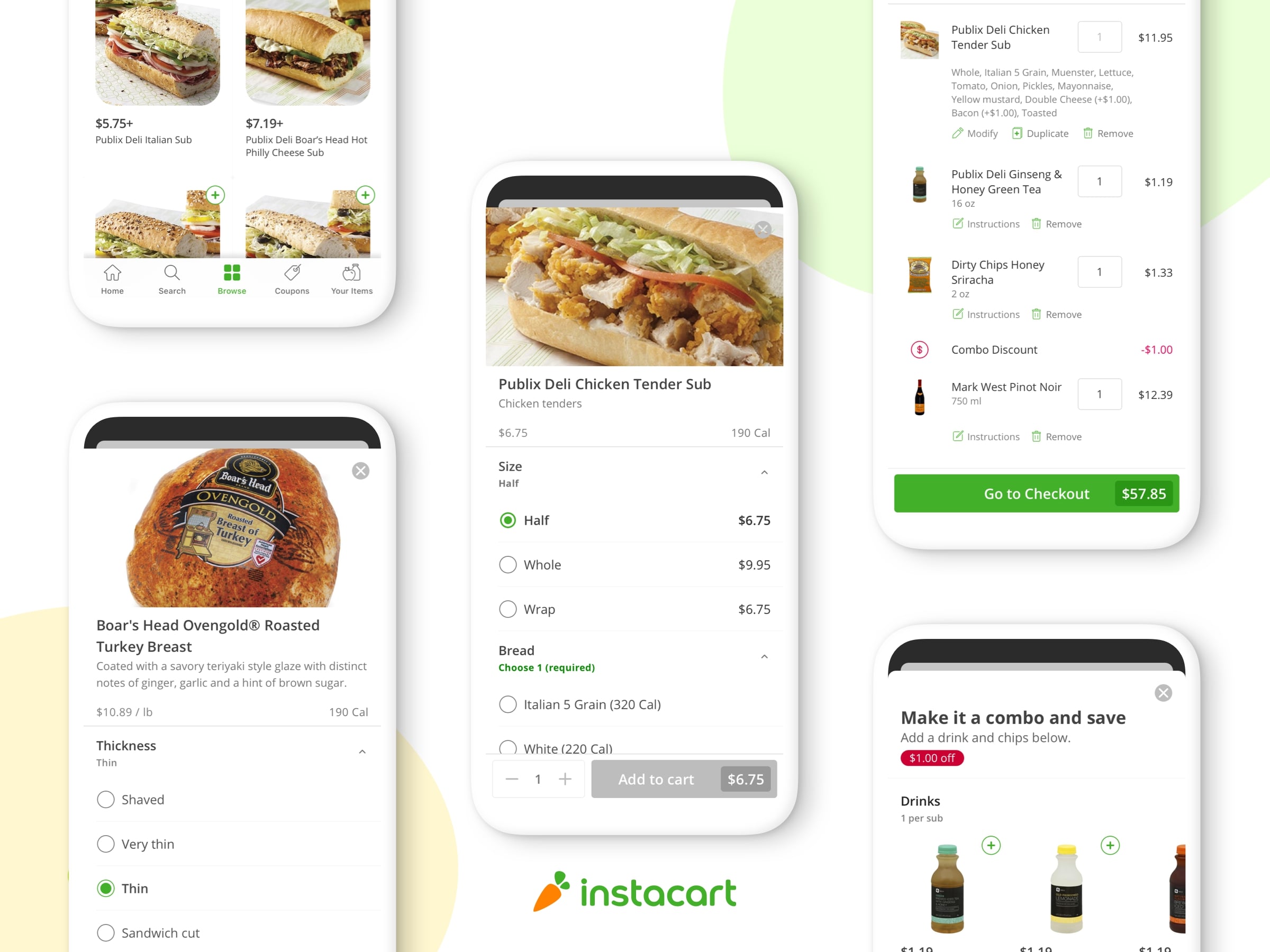
図3. Instacartの配送オプションの在庫状況と価格情報の図。

下記の例をご覧ください（Figure 3）。“一時間以内”と“二時間以内”の選択肢は“1–2pm”よりもっと高いです。

私たちは「消費者が基本的に早めの配達が好きです」この事実を知っています。だから、もし二つの選択肢が同じ値段の場合だと、消費者は“一時間以内”を選ぶ可能性がより高いです。

この記事の残りの部分では、私たちは伸縮需要の量を想定し、それを最適化する方法に焦点を当てます。

予測のための弾力的な需要の数値

 表1の例では、パターン2の9-10での10単位の需要は伸縮性があり、10-11に再配分することができると仮定します。図4に示すように、新しい需要は、9-10で10と20との間、10-11で20と30の間の任意の整数値とすることができます。

図4.9-10には10単位の伸縮需要があり、サブセット（0％-100％）は10-11に再分配できます。

伸縮需要を考慮すると、表3に示すように、両方の予測は期待コストが小さく、予測2はゼロのコストです。

表3. パターン2を考慮した2つの予測の予想コストは、10単位の弾性需要を有する。

Elastic demandを活用する

こちらの例を見てください。二つのタイムシリーズ（需要系列として）があって、三つの時間帯があります。私たちはこの需要系列の差を縮めたいです。仮に各時間帯の需要系列は10件の伸縮需要があり、その10件の需要も隣接する時間帯に移動できます。私たちが需要を再分配して、二つのシリーズを同じにすることができます。Figure 5 (真ん中)は５つのユニットをT1 から T2に移動した結果です。Figure 5 (右)はT2 から T3の結果です。

                  図5.弾性需要を再配分して、2つの需要系列を同一にする。

例えば、私たちはゴール、インプット、アウトプットを概括できます：

• ゴール：ちょうどいい数の伸縮需要を移動し、新たな需要系列間の差を縮めていきます。
• インプット：昔のデータシリーズと伸縮需要の数です。
• アウトプット：移行した需要系列です。

我々は、伸縮需要が隣接するタイムスロット間でのみシフトできるという制約を伴って、以下の公式を提案する。

Part 1掛けるPart 2の結果は需要がt-1 から tに移動した結果です（kth series）

Part 3は、ある量がtからt + 1にシフトした後のtにおける残りの需要を表す。

つまり、Part 4はtである新た需要です（kth series）。

Part 5は、新しい需要系列の需要予測であり、Part 6は、すべてのtの見積もりに対する二乗誤差の合計です。 Part 6を最小化することは、新しい需要系列間の全体的な分散を最小限にすることと考えることができます。

Part 7はdemand shapingのコストを見られます。

Part 8はkth seriesのelastic demandの数です。L (≤0)の場合はelastic demandが左側の時間帯に移行できます。U (≥0)の場合は右側の時間帯に移行できます。

Part 9はdemandの予想をマイナスにならないようにします。

これは、グローバルに最適な解を持つ最適化問題です。

結果

図1（左）に示す需要系列に伸縮需要の最適化を適用し、伸縮需要の割合をそれぞれ10％、20％、30％、40％、50％としました。ここでは、すべてのシリーズのタイムスロットに対して同じ割合の伸縮需要を使用します。

元の需要系列と新しい需要系列を図6に示します。弾性需要を考慮すると、1時間ごとの需要系列の分散が小さくなり、予測がより効果的になります。

図6.伸縮需要のさまざまなパーセンテージに対するオリジナルの需要系列と新しい需要系列。

図7は、図6の需要系列の各グループの平均時間需要分散を示しています。予想通り、弾力需要量が多いほどばらつきは小さくなります。しかし、最初の10％の伸縮需要は、最大の分散減少をもたらす。

図7.伸縮需要のさまざまなパーセンテージにおける平均時間需要分散。

結論

大きな需要の変動は、販売機会の喪失または過剰供給のために高いコストをもたらす可能性があります。われわれは歴史的な伸縮需要を再配分して分散を減らし、需要予測と供給計画をより効果的にすることができることを示しました。

Instacartは毎時間配信ウィンドウを実装しているため、毎日のサイクルで時間ごとの需要に注目し、同じ日から隣接する時間帯に伸縮を再配分できると仮定します。曜日の季節性がある場合、提案された方法は、別々の曜日からの需要系列に別々に適用することができます。

毎週のサイクルまたは毎年のサイクルで毎日の需要を処理するためにメソッドを拡張するには、サイクルの最後から次のサイクルの開始まで伸縮需要がシフトできるように、配合を変更する必要があります。

注：Dong Liangは、2011年1月30日から2011年6月16日までのInstacart在籍中、この仕事に貢献しました。

タイトル：Leveraging Elastic Demand for Forecasting

作者：Houtao Deng

原文URL: https://tech.instacart.com/leveraging-elastic-demand-for-forecasting-6278b45f805f