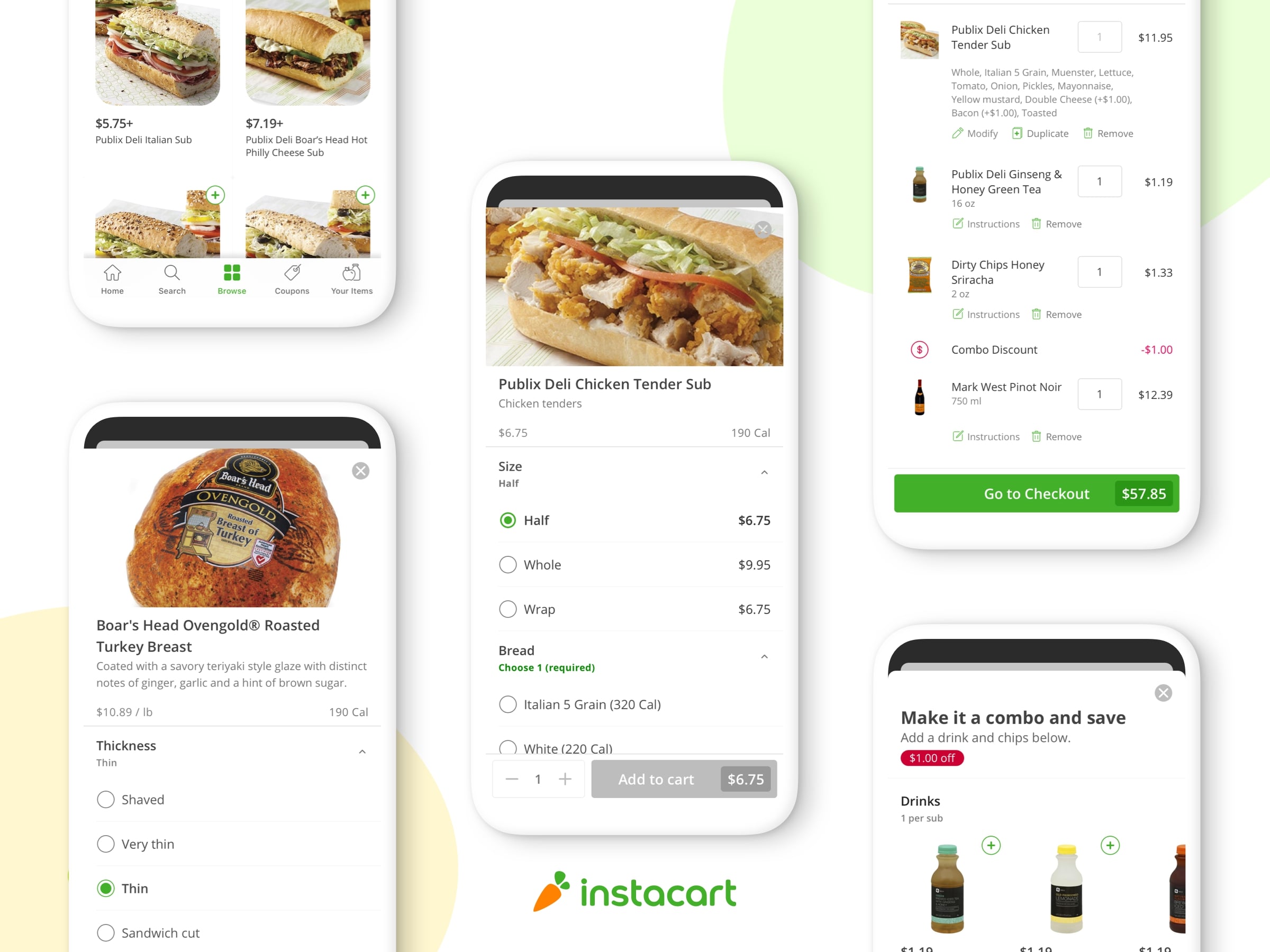
分散を管理し、定刻の配送を確実にするために、分位回帰をどのように使用するか。

Instacart配信メールリマインダー。

Instacartでは、多くの食料品を提供しています。 まもなく、80％のアメリカの家庭でInstacartを使うことができます。 以前のブログ記事Space、Time and Groceries（ジェレミー・スタンリー）では、ロジスティクスの問題がどれほど複雑であるかを話しました。 特に、タイムウィンドウ付き動的キャパシティ車両ルート問題（DCVRPTW）を解決する必要があります。 目標は、時間通り効率的な方法で注文が確実に届くようにすることです。

当社のフルフィルメントアルゴリズムは、shoppersを食料雑貨品店（スーパー）に誘導して食料品を選び、顧客の家に1時間以内に届ける方法をリアルタイムで決定します。

注文を行うためには、shoppersは店に行って、食料品を選んで顧客の場所に届け、配送を行う必要があります。

Shoppersのルートを最適化するには、Shoppersが指定された注文をどれくらいの時間を費やすかを知る必要があります。 これが配達時間を予測するモデルを構築した理由です。 この予測モデルに組み込まれる正確な機能とモデルの構築方法は、このブログ記事の目的ではありません。 むしろ、このモデルがフルフィルメントエンジンによってどのように使用されるかについて、深く掘り下げて学習します。

顧客が午後1時〜2時に注文したとします。 つまり、到着予定時刻（ETA）が1pmから2pmになるように配達計画を立てる必要があるということです。 午後1時前に注文は早い、午後2時以降に注文が遅れると見られます。

時間通りに配達される予定の例です。つまり、ETAは期限前です。

しかし、注文が時間通りに配達されるようにするには、期限（2pm）前にETAを設定するだけでは不十分です。 私たちは、shoppersが期限前に実際に注文を届くことを望みます。

実際に時間通りに届く注文の例、すなわち実際の到着時刻は、到着予定時刻より前です。

言い換えれば、注文が実際に時間通りに提供されるようにするには、次のものが必要です。

実際の到着時間= ETA +予測エラー<期限

Actual Arrival Time = ETA + Prediction Error < Due Time

当然のことながら、注文が届くまで予測誤差はわからないので、予測誤差の大きさを考慮する方法が必要です。 私たちの予測モデルが偏っていなくても、私たちは平均で修正するだけです。つまり、誤差の分布が広くなる可能性があります。 以下は、異なる都市における予測誤差の分布です：

モデル誤差の分布。 エラー=実際の予測

したがって、これを説明するために、モデル予測誤差をカバーするために使用されるバッファ（Buffer）の概念を紹介しましょう。 したがって、shopperへの配達を計画するときは、次のようなバッファを使用する必要があります。

ETA +バッファ<所要時間

ETA + Buffer < Due Time

ここで問題となるのは、このバッファにはどのような価値がありますか？

バッファは、ほとんどの場合、遅れのリスクをカバーするために十分高い数値が必要となります。 しかし、バッファーが高すぎると、最適化問題の実現可能なスペースのサイズを減らすことで効率が低下する可能性があります。

シンプルなアプローチ

一番単純な解決策として、配達予定日程（時間）にどれくらいの遅れがあるかによって、配達遅延の割合を調べました。

遅れのパーセンテージは、配達予定時間に近いところに依存します。

たとえば、サンフランシスコでは、ウィンドウがクローズ10分前にすべての配達が届く予定がある場合、配達の約18％が遅れていることがわかります。

私たちは、遅れの最大限のパーセンテージに基づいて固定バッファを選択しました。 上記のグラフを見て、最悪の場合は約10％の遅配が発生するのを設定し、バッファを選択しました。 このアプローチを使用して、シカゴ・ノースの場合は13分、マンハッタンの場合は15分、サンフランシスコとマイアミの場合は18分を選択しました。

しかし、このアプローチは明らかに最適ではありませんでした。 リスクが高い場合と、リスクが低い場合があります。 したがって、固定バッファは時にはあまりにも保守的であり（遅れのリスクが高い）、ときにアグレッシブである（効率の損失）ことがあります。

より良いアプローチは、配達時間の予測間隔を計算し、間隔の上限を使用することです。 これは、分位回帰が作用するところです。

Quantile regression（分位回帰）

まず、分位回帰について説明しましょう。

典型的な回帰は、分布の平均に合わせることを目的としています。 予測変数Xの特定の値が与えられたときの応答変数yの条件平均を近似しようとする。この文脈において、目的は最小化することである。

y_iは予測される変数のi番目（ith）の値、yhat_iはy_iの予測値です。

分位回帰では、ある分位qについて、真の値のq％がQよりも小さくなるように、一連の予測Qを作成します。この場合、次の損失関数を最小にしようとします。

特別な場合q = 0.5は、費用関数が絶対偏差である中央回帰（median regression）に対応する。

異なるqの値に対する線形回帰と量子化回帰のコスト関数。

距離の関数として、配送時間を予測する単純な線形モデルを構築したいと仮定しましょう。

距離の関数としての配送時間を予測する線形回帰

分位回帰では、納期の予測間隔を得ることができます。 下限についてはq = 0.1を選択し、上限についてはq = 0.9を選択しましょう。

予測間隔として使用される配達時間については、クォンタイル回帰q = 0.1およびq = 0.9である。

分位の回帰が納期の予測間隔を与えることがすぐにわかります。 予測間隔は、配達距離が増えるにつれて増加することがわかります。これは、遠距離では正確に予測するのが難しくなります（分散が大きく、データが少ない）。 したがって、この予測間隔は、平均予測値（単純アプローチの固定バッファ）にグローバル定数を追加するよりもはるかに優れていることがわかります。

問題に戻りましょ

私たちの場合、2番目のモデル、q = 0.9分位回帰を構築しました。 このモデルは、配達時間の上限を与えます。配達時間が90％も遅れることはありません。 shoppersに納品を発送する際には、次のものが必要です：

第90象限からの予測<納期

Prediction from 90th quantile < Due time

複数な配達

現実には、フルフィルメントエンジンは、shoppersの時間を無駄ないように、そしてシステムの効率を上げるために、最大5つの注文を含む配達を生成しようとします。

このタイプの配達を計画する際には、すべての注文が時間通りに提供されることを確認し、遅れのリスクを管理する必要があります。 このリスクは累積的です。 たとえば、shoppersが１つの注文に対して予想以上に時間がかかる場合、これは他残りの配達に影響を与えます。

この累積リスクを考慮するために、特定の配達に使用する必要があるバッファは、以前の配達のバッファの関数である必要があります。 まずは２つ注文があるの配達の例をご覧ください、すなわち１回の配達でD1とD2２つの注文を含む配達を考えてみましょう。

例はこちらになります

Dt0->1 = Predicted delivery time from store to D1.
Dt1->2 = Predicted delivery time from D1 to D2.
Qt0->1 = 90th percentile prediction from store to D1.
Qt1->2 = 90th percentile prediction from D1 to D2.
B0->1 = Qt0->1 – Dt0->1 = Delivery Time Buffer from store to D1.
B1->2 = Qt1->2 – Dt1->2 = Delivery Time Buffer from D1 to D2.
B0->2 = Buffer that we need to use to make sure D2 will not be late.

D2が期限前に届くされるようにするために必要なバッファB0-> 2を計算する必要があります。

Dt0->1 + Dt1->2 + B0->2 < Due Time of D2

独立した通常の確率変数としての配送時間。

Dt0-> 1 + Dt1-> 2 + B0-> 2 <D2の経過時間

2つの独立した正規乱数変数の和は、依然として正規分布に従います。

2つの正規の独立したランダム変数の和

正規分布の場合、予測区間は[μ – z *、μ+ z *]（90％予測区間ではz = 1.67）として簡単に計算できることがわかります。 つまり、

D1とD2の個々のバッファからD2の合計累積バッファを計算する定式。

最後に、次の定式を使用してN配達に一般化することができます。

配達についてN番目の配達のための累積バッファの一般化。

結果

quantile regressionと固定バッファを使用するときの効率/遅れのトレードオフへの影響を測定するためにA / Bテストを行った。

分位回帰では、遅いパーセンテージを増やすことなく、予定時間に近づける計画を立てることができます。

上記のグラフからわかるように、分位回帰では、遅いパーセンテージを増やすことなく、配達時間をより正確に計画できることが分かりました。 この効果により、フルフィルメントエンジンでより多くの旅行の組み合わせを探索し、効率（当社の最も重要な指標の1つ）を4％向上させることができました。

結論

多くの予測問題では、平均を超えて考える必要があるかもしれません。 Quantile回帰はそのための非常に強力なツールです。分布のパーセンタイルを近似できるので、変数間の関係をより包括的に分析することができます。 Instacartでは、遅れ配達のリスクをよりよく理解し管理するために、分位回帰が使用されています。

Instacartで働きたいですか？ ここに申請してください。

Instacartの仕事についてもっと知りたいですか？ ここをクリックしてください。

タイトル：How Instacart delivers on time (using quantile regression)

作者：Mathieu Ripert

原文URL: https://tech.instacart.com/how-instacart-delivers-on-time-using-quantile-regression-2383e2e03edb